무손실 조인 분할
무손실 조인 분할은 릴레이션을 분해한 후에 다시 조인 연산을 수행하도 데이터 손실이 없도록 릴레이션을 분할하는 방법입니다.
함수 종속성
-
Functional Dependency
-
t₁[α] = t₂[α]이면 반드시t₁[β] = t₂[β]가 성립하는 경우, α → β 성립→ α 부분이 같으면, β 부분도 같다가 성립하면 α → β 종속성이 존재 (역은 성립 X)
함수 종속성 집합의 Closure
-
함수 종속성 집합 F의 closure: F+
F에 의해 논리적으로 유도될 수 있는 모든 함수 종속성들의 집합
-
단순 종속성( Trivial Dependency )
속성 α가 속성 β를 포함하면, α → β는 단순 종속성
-
부분 종속성( Partial Dependency )
→ α → β가 성립하며, γ ⊂ α인 속성 γ에 대해 γ→β 도 성립한다면, β는 α에 부분적으로 종속
-
Armstrong Axioms
- 함수 종속성 규칙
| 특성 | 설명 |
|---|---|
| 반사 | If β ⊆ α, then α → β |
| 첨가 | If α → β then αγ → βγ |
| 이행 | If α → β and β → γ then, α → γ |
| 결합 | If α → β and α → γ then, α → βγ |
| 분할 | If α → βγ, then α → β and α → γ |
| 의사 이행 | If α → β and ωβ → γ, then ωα |
예제
-
예제 1
- A → C : 성립 X (같은 α3이 없음)
- AB → D : 성립 O (같은 α 부분이 없음 - 전제가 거짓이므로 항상 true)
-
예제 2
R = (A, B, C, G, H, I)
F = {A → B, A → C, CG → H, CG → I, B → H}
F+에 포함되는 종속성들
-
A → H
A → B, B → H
-
CG → HI
CG → H, CG → I
-
AG → I
A → C ⇒ AG → CG. CG → I
-
속성 집합의 Closure
-
속성 α의 closure: α+
α에 함수적으로 종속되는 모든 속성들의 집합
A+ = ABCH
(AG)+ = ABCGHI ← R의 후보 키
Canonical Cover
-
정규 커버(=최소 커버)
-
관계형 데이터베이스에서 스키마의 변경이 발생할 때마다 함수적 종속성(FD)의 유지 여부를 검사함
→ 따라서 Closure이 동일한 여러 개의 함수적 종속성이 존재하는 경우, 가능한 한 단순한 종속성을 선택하여 구현하는 것이 좋습니다.
- e.g. A → C이고 AB → C이면, B는 생략 가능
정규화
이상현상 (Anomaly)
- 삽입 이상(Insert Anomaly) : 계좌가 없는 Branch 정보를 입력할 수 없음
- 삭제 이상(Delete Anomaly) : L-29 계좌 삭제 → Pownal 지점 정보 삭제
- 갱신 이상(Update Anomaly) : Downtown 지점의 Asset이 변경됨
목표
- 이상 현상(Anomaly) 제거
- 테이블 간 중복 데이터를 허용하지 않고 저장 공간의 최소화
- 데이터 구조의 안정성 및 무결성 유지
단점
- 정규화시 테이블의 개수 증가
- 릴레이션 간의 JOIN 연산 증가 → 질의에 대한 응답 시간 저하
무손실 조인 분할
- 분할시, 사라지는 속성이 있으면 안됨
- 분할하고 조인했을 때, 분할 전과 동일해야 함
종속성 보존 분할
DB 갱신 연산시 함수 종속성 만족 여부 검사
릴레이션 R이 R1, R2, … Rn으로 분해 되었을 경우, 함수적 종속 집합 F도 각 릴레이션에 속한 속성만을 포함한 함수적 종속 집합 F1, F2, …, Fn으로 분해
정의
F’ = F₁ ∪ F₂ ∪ … ∪ Fₙ
F’ = F+ 이면, 종속성 보존 분할
정규화 단계
정규화는 일반적으로 1NF(제1 정규형)부터 5NF(제5 정규형)까지 여러 단계로 이루어집니다.
제 1 정규화
제1 정규화란 테이블의 컬럼이 모든 속성이 원자 값(atomic value)만을 갖도록 하는 것입니다.
제1 정규화는 부분 종속성(Partial dependency)이 있을 수 있습니다. 주 키가 있으면, 이에 종속적인 속성이 있다는 뜻입니다.
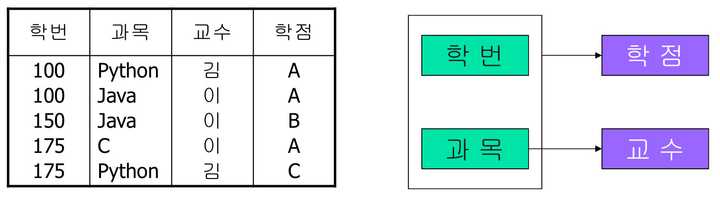
주 키가 존재할 때, 주 키에 속하는 일부 속성들이 종속적으로 존재하는 경우 이를 부분 종속성이라고 합니다.
간단히 말하면, 주 키를 구성하는 일부 속성이 독립적으로 존재할 수 없고, 주 키 전체에 종속적인 상태를 나타냅니다.
위 테이블의 주 키는 학번, 과목입니다. 그런데 주 키의 부분 집합중 하나인 과목에 대해 교수 속성이 종속적입니다. 즉, 과목 → 교수 속성이 존재합니다.
제 2 정규화
제2 정규화는 제1 정규화를 거친 테이블에서 완전 함수 종속을 만족시키기 위해 테이블을 분해하는 단계입니다. 완전 함수 종속이란 결정자로 주 키의 부분집합이 되어서는 안 된다는 것을 의미합니다. 즉, 주 키에만 모든 속성이 종속적이라는 것을 의미합니다.
제 1 정규화에시로 나타낸 테이블은 아래와 같이 부분 종속성을 없앨 수 있습니다.
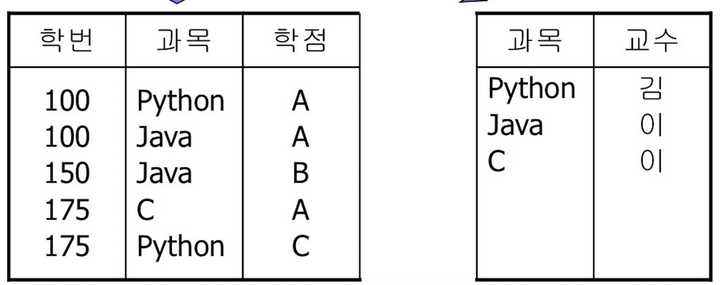
위의 예시에서 부분 종속성을 없애 제 2정규화된 테이블
이렇듯 과목 → 교수 종속성을 다른 테이블로 분리해서 완전 함수 종속성을 만족합니다.
제 3 정규화
제 2 정규화는 부분 종속성은 없애지만 이행 종속성이 존재할 수 있습니다.
- 이행적 종속이란 A → B, B → C가 성립할 때 A → C가 성립되는 상황을 의미
제3 정규화는 제2 정규화를 거친 테이블에서 이행적 종속을 없애기 위해 테이블을 분해하는 단계입니다.
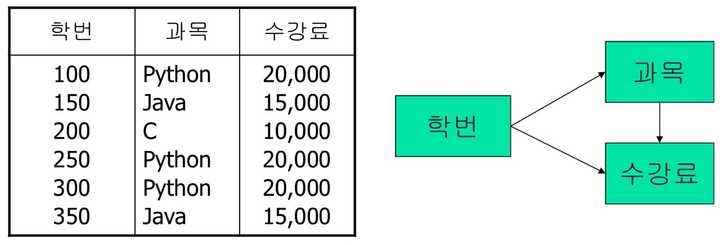
위와 같이 이행 종속성(transitive dependency)가 존재합니다.
- 학번 → 과목: 학번에 따라 어떤 과목을 수강했는지 알 수 있습니다.
- 과목 → 수강료: 특정 과목을 수강하면 그 과목의 수강료를 알 수 있습니다.
- 학번 → 수강료: 학번을 통해 어떤 과목을 수강했는지 알 수 있고, 그 과목의 수강료를 알 수 있습니다.
여기서 학번이 수강료에 이행적으로 종속되는 것을 확인할 수 있습니다. 즉, 학번을 통해 간접적으로 수강료를 알 수 있습니다.
테이블을 분리해서, 학번 → 과목, 과목 → 수강료 종속성만 남겨 이행 종속성을 없앨 수 있습니다.
BCNF 정규화
- BCNF 정규형은 데이터베이스의 테이블이 1NF(제 1 정규형), 2NF(제 2 정규형), 3NF(제 3 정규형)를 만족하면서 추가로 식별자로 쓰이는 속성이 일반속성에 종속되지 않아야 함
- 즉, 3NF를 지키면서, 모든 결정자가 후보키 집합에 속해야 함
-
예제. BCNF가 아닌 제 3 정규화된 테이블
Customer-name Branch-name Banker-name Jones Perryridge Johnson Smith Perryridge Johnson Hayes Perryridge Johnson Curry Redwood William Turner Redwood William 주 키에 포함되지 않는 속성(Banker-name)에서 주키의 일부 속성(Branch-name)으로 함수 종속성이 존재합니다.
BCNF로 정규화하기 위해서는 주 키가 아닌 컬럼에서 주 키로 향하는 종속성을 제거해야 합니다.
e.g. Banker-name → Branch-name 종속성
BCNF로 무손실 조인 분할 방법
-
R의 주 키가 아닌 어떤 속성 α가 다른 속성 β에 영향을 미치는 경우
→ Suppose non-trivial dependency α → β, where α is not a super key for R.
위의 예제에서는 Banker-name → Branch-name 종속성
-
릴레이션 R을 R1 = (α, β)과 R2 = (R – β)로 분할
-
위의 예시 테이블을 BCNF로 정규화하기
2개의 릴레이션으로 나눌 수 있습니다.
- (Customer-name, Banker-name)
- (Banker-name, Branch-name)
Customer-name Banker-name Jones Johnson Smith Johnson Hayes Johnson Curry William Turner William Banker-name Branch-name Johnson Perryridge William Redwood BCNF로 정규화된 릴레이션은 무손실 조인 분할이지만, 종속성 보존 분할은 아닐 수도 있습니다.
정리하면, BCNF 정규화는 테이블에서 모든 결정자가 후보 키의 일부인 경우에 해당하는 정규형입니다.
제 4 정규화
다중치 종속성
α 값에 따라 β 값의 종류가 결정되는 것을 볼 수 있습니다. 이를 다중치 종속성이라고 합니다.
α →→ β
제 4정규형은 BCNF보다 더 제약을 많이 받고 있으며, 모든 제 4정규형은 BCNF에 포함됩니다. 일반적으로 모든 테이블은 제 4정규형으로 전환될 수 있습니다.
- 과목→→교수, 과목→→교재
위의 릴레이션은 BCNF로 정규화되었지만 정보의 중복(과목, 교재)이 발생합니다. 이는 모든 속성이 원자값이기 때문입니다.
제 4 정규화한다면, (과목, 교수) & (과목, 교재)로 나눌 수 있습니다.
제 5 정규화
정리
정규화 수준이 높아질수록 요구하는 사항들이 늘어나, 릴레이션을 잘게 쪼개는 것을 볼 수 있었습니다.
| 단계 | 설명 |
|---|---|
| 제 1정규화 | 속성은 원자값이어야 함 |
| 제 2정규화 | 완전 함수 종속을 만족, 부분 종속성이 없어야 함 |
| 제 3정규화 | 위의 조건을 만족하며, 이행 종속성이 없어야 함 |
| BCNF 정규화 | 식별자로 쓰이는 속성이 일반 속성에 종속되지 않아야 함 |
| 제 4정규화 | 다중치 종속성이 없어야 함 |
|제 5정규화 | 릴레이션 R의 모든 조인 종속성의 만족이 R의 후보 키를 통해서만 만족 |
다만, 너무 과도한 정규화는 데이터베이스 쿼리의 복잡성을 높일 수 있고, 많은 조인으로 성능에 나쁜 영향을 줄 수 있습니다. 그러므로 적당히 타협해서 정규화 수준을 정하는 게 좋을 것 같습니다.